Whole-Body Control of Biped Humanoid Robots (2006-2010)
This page describes a past study on whole-body motion control of torque-controlled humanoid robots conducted in research projects at ATR-CNS, Japan. Note the contents presented here are related only to classical model-based motion control, and do not include data-driven ones (e.g. reinforcement learning) also studied in the same projects. See the official website of the ICORP Computational Brain Project.
- Contents -
Results:
- Full-body torque control
- Full-body force control / Gravity adaptation
- Full-body compliant balancing
- Phase transition / Static walking
- Push-recovery
- Dynamic walking
- Baseball batting
What's New:
- (2010/9/8) This page has been moved from a ATR server to Ritsumeikan server to make it easy for the administrator to update the contents. All the contents (photo, videos) are with ATR and/or NICT.
- (2010/5/5) Our work "From compliant balancing to dynamic walking on humanoid robot: Integration of CNS and CPG" was selected as the Finalist for the IEEE ICRA 2010 Best Conference Video Award.
- (2010/5/5)
This work has been introduced in 2010 IEEE International Conference on Robotics and Automation (ICRA) Workshop on active force control for humanoid robots.
We invited top runners from Boston Dynamics, Honda, Disney Research, ATR, DLR, USC, Stanford Univ. to discuss together on state-of-the-art force control technologies applied to humanoid/legged robots. - (2009/5/16) Our recent paper "Integration of multi-level postural balancing on humanoid robots" was selected as the Finalist for the IEEE ICRA 2009 Best Conference Paper Award.
- (2008/9/10) Young Investigation Excellence Awards given by Robotics Society of Japan.
- (2008/5/23) A new control/learning framework presented at IEEE ICRA2008.
- (2008/5/4) A baseball batting demo on CB-i introduced in NHK Special.
- (2007/12/6) Article "Balancing Robot Can Take a Kicking" on Slashdot
- (2007/12/6) Article "Flexible-jointed robot is no pushover" on NewScientistTech
- (2007/10) The full-paper on compliant balancing and interaction under unknown disturbances was published on IEEE TRO, vol.23, no.5.
- (2006/12/4) Some experimental results were presented at IEEE-RAS Humanoids2006.
- (2006/5/27) Full-body compliant balancing under unknown disturbance was achieved on a SARCOS biped humanoid robot.
Research Objectives:
- Understanding human motor control and learning especially focusing on postural control and biped walking
- Realization of hyper performance humanoid/legged robots
- Elucidation of versatile locomotion with dynamical stability
- Development of computationally-plausible assistive devices for humans
Platform:
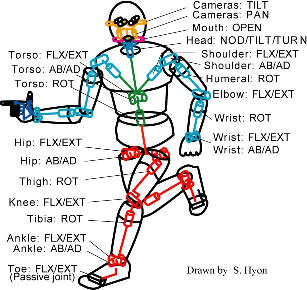
Joint configuration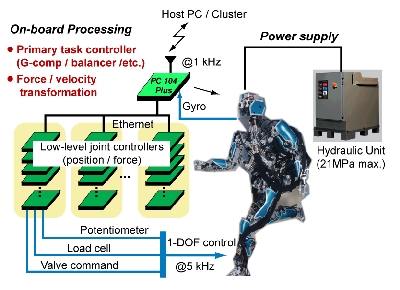
Experimental system
For more technical details of the platform, see:
Cheng, G., Hyon, S., Morimoto, J., Ude, A., Hale, J. G., Colvin, G., Scroggin, W. and Jacobsen, S. C., CB: A humanoid research platform for exploring neuroscience, Advanced Robotics, vol.21, no.10, pp.1097-1114, 2007.
Framework:
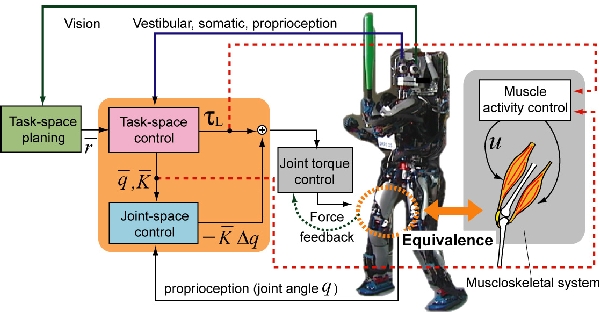
We test our hypothesis of motor control and learning of humans by testing possible hierarchical computation and body structures on a full-body humanoid robots, especially focusing on the function of the task-space controller, joint-space controller, and musculoskeletal systems, as shown in the figure below. The former is supposed to be in the central nervous system (CNS), and the second in the central pattern generator (CPG) or lower reflex centers. Not only testing hypothesis of each module, but also investigating how these three modules are combined effectively to achieve optimal motor control performance in different contexts is our primary research interest.
Results:
Full-body torque control
We first implemented joint torque controllers using the force sensors attached to the joints. This enabled us to develop several motor control algorithms in which the control input is defined as the joint torque. Also this enabled us to functionally emulate human musculo-skeletal system, which can control load and stiffness simultaneously.
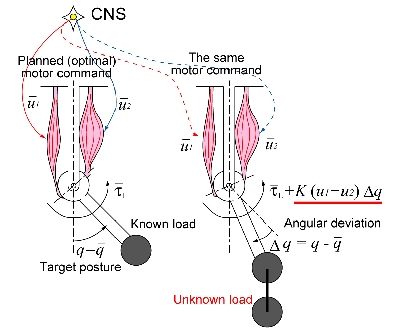
The extra benefit is that we can easily simulate the robot behaviors on multi-body dynamic simulators without considering the actuator dynamics which are required in conventional position-control-based robots. The joint torque controller is designed according to the actuator dynamics including hydrostatic dynamics. With the full-body torque controller, the robot can make its limbs free, or gravity-compensated to passively follow external forces applied by humans. This is a fundamental function for natural and safety interaction between humans and robots.

Moreover, with the gravity compensation, fast joint motions can be achieved by superposing joint trajectory tracking controllers with very roughly-tuned PD gains.

Since the gravity compensation requires internal model of the body and vestibular feedback, it is natural to assume the function is implemented in the central nervous systems (CNS) of humans, not in any other low-level nervous systems.
Full-body force control / Gravity adaptation
Humans can stably stand on rough terrain by applying forces to each foot or hand. So, we developed a practical control algorithm that can optimally control the multiple contact forces between the robot and the ground simultaneously.
Our computational procedure is simple as follows:
1) Compute the desired global ground applied force (GAF),
2) Optimally distribute that force into the multiple contact points,
3) Convert the multiple contact forces into the whole-body joint torques,
4) Add joint-wise damping to suppress internal motions.
Step 4) is called as a passivity-based redundancy resolution, which is a simple, but important concept in redundant robots (but tuning appropriate damping is not straightforward). The full-body gravity compensation while standing is achieved by commanding the anti-gravity force as the desired global GAF in the step 1). Then, the robot behaves like "clay"; passively adapts to external forces and surrounding surface (see the next section).
Full-body compliant balancing
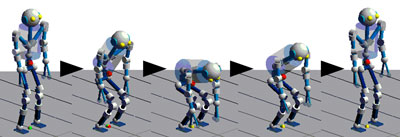
We can specify some desired center of mass (CoM) motions (time course of acceleration, velocity, position), and convert them into the desired GAF in a feedforward or feedback form in the algorithm 1) in the last section. If we set the desired CoM position to zero, the algorithm serves as a full-body balancing controller. Since the robot has redundant joints, the balancing behavior is compliant in the sense that the robot can move freely in the range of motions while keeping the CoM to the desired position, as can be seen in the left figures.

The load distribution to the both feet is optimally determined by the algorithm 2). When the robot CoM is shifted to one side, the center of pressure (CoP) is shifted to the same side, and the contact forces distribution is shifted accordingly. This may cause the contact forces of the other side foot to zero, resulting in the lift off when the leg is fully extended as can be seen in the left figure, where the human is pulling the robot to left side. After the touchdown, the robot is balancing at the new contact points.

Thanks to the vestibular feedback, the robot can balance on randomly moving seesaw. The vestibular feedback is used in the algorithm 4) and the CoM estimation. When the seesaw changes its inclination, the robot foot instantaneously lose its contact if the robot is stiff. This is not our case because our controller is force-based, implemented the optimal load distribution, hence has natural terrain adaptability (see also the next section).

If we superpose some joint-trajectory tracking controller to the null-space of the task-space controller, the desired joint motions are achieved with the secondary priority. For example, sinusoidal ones. Periodic sway, or squat motions can be easily created.



- Torso bending (0.5 Hz) showing the superposed torso motion is automatically compensated by the balancing controller.
- Squat with the upper-body swinging showing the superposition of the CoM tracking controller and the (joint-level) trajectory tracking controller of the torso
- High-speed squat on one-foot showing the superposition of the CoM tracking controller and the (task-space) position controller of the one foot
Also, the desired contact points can be added or removed so that the robot can take toe-off or heel-off contact.
Some experimental videos are available from the supplemental material for our papers:
Phase transition / Static walking
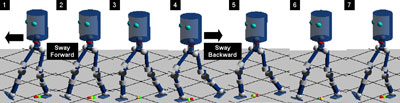
The robot can transit from double support (DS) to single support (SS) by shifting the desired CoM position and making the contact switching. For example, we can use a smooth target CoM trajectory (sinusoidal). When the CoM velocity exceeds the threshold determined by the saddle condition of the inverted pendulum model, we remove the contact from one foot. The transition from SS to DS (touchdown) is done in a feedforward manner; the robot simply switches its controller from SS balancing to DS balancing, regardless of the actual touchdown, once the decision of the phase transition has been made (hence the prediction is important). The swinging leg trajectory is not given. Thanks to the innate terrain adaptability of our controller, the robot can land or even stand on wooden blocks of the moderate size.

If we do not specify the CoM height or the knee angle, the supporting leg has compliance even during the one-foot balancing because the robot is gravity compensated. In the same way, the swinging leg can bee freely moved by hand unless some trajectory tracking controllers are applied to it. The ability of balancing at single and double support phases and of transition between them means that the robot can perform static, or quasi-dynamic biped walking. Actually, forward/backward walking have been achieved as shown in the left figure without any technical difficulties. Wherein, the swinging foot position is commanded by the operator's key inputs, and the desired CoM position is fixed to the center of the supporting foot, except for when the transition from SS to DS is made (therefore this is a quasi-dynamic walking).


With exactly the same controller, the robot can also climb steps with the moderate height (kicking motion is required for higher steps).
 Return to top
Return to top
Push-recovery control
Physiologists have been discussing human push-recovery strategies based on experimental data of humans. There are ankle strategy, hip strategy, and step strategy. It is of our interest how and where these strategies are implemented in our nervous system and body, and when these are switched according to various unstable situations. Therefore, we studied such strategies from control point of view and experimentally implemented them on our humanoid robot.
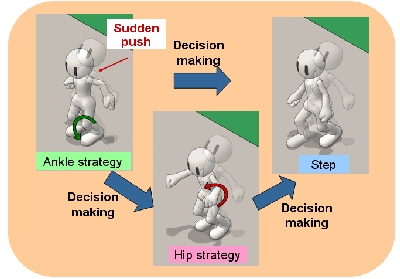 The ankle strategy can be extended to the full-body balancing controller described above because our controller can be considered as the full-body reflex including the reflex by the ankle stiffness, where we used static internal model and simple dynamic inverted pendulum model. On the other hand, the hip strategy is useful when the CoM is out of the support region. In this case, the system becomes underactuated and relatively high nervous cost may be required. We implemented the hip strategy based on an underactuated double-pendulum model. We didn't make any switching between the ankle and hip strategies, but combined the both with the simple torque superposition. One can see the rotational motion of the upper body is relatively larger than when only the "ankle strategy" is employed. With this integration, the region of attraction of CoM was enlarged (but the computational cost increased).
The ankle strategy can be extended to the full-body balancing controller described above because our controller can be considered as the full-body reflex including the reflex by the ankle stiffness, where we used static internal model and simple dynamic inverted pendulum model. On the other hand, the hip strategy is useful when the CoM is out of the support region. In this case, the system becomes underactuated and relatively high nervous cost may be required. We implemented the hip strategy based on an underactuated double-pendulum model. We didn't make any switching between the ankle and hip strategies, but combined the both with the simple torque superposition. One can see the rotational motion of the upper body is relatively larger than when only the "ankle strategy" is employed. With this integration, the region of attraction of CoM was enlarged (but the computational cost increased).

Furthermore, we implemented a heuristic step strategy, where the robot takes step to recover the balance at the next support phase when the push is too strong (threshold has been set).Herein, the one leg is swung symmetric to the CoM, hence the motion of the swinging leg is synchronized to that of the CoM. The robot may take multiple steps according to the magnitude of the push, which is shown in the simulation movies.
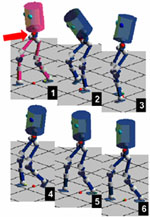
- Integrated balancer showing the combined ankle and hip strategies
- Disturbance rejection with stepping
The experimental videos are available from the supplemental material for our papers: IEEE ICRA, 2009
Dynamic biped walking
Up to simulations, it is found that biped walking that is robust to the external disturbances can be simply achieved by superposing the above mentioned symmetric step strategy onto the full-body balancing controller under the velocity control mode. If we turn off the balancing controller, then the robot is purely gravity compensated. With the symmetric stepping, however, the robot can walk at almost constant velocity. When pushed, the robot changes its moving direction, just like a "ball" rolling on a flat surface (globally stable). We call this Symmetric Walking Control. The theoretical discussion can be found in our paper. When we activate the velocity controller together with the above controller, then the robot can walk at the specified speed and direction. This is our passivity-based control solution for globally asymptotically stable walking (gait generation).
[Simulations]- Symmetric Walking Control: Externally-driven walking showing the walking gait is (Lyapunov) stable
- Symmetric Walking Control: Speed-regulated walking showing the walking gait is asymptotically stable
Although the above simulations show the effectiveness of our control method for stable walking, the controller requires relatively precise tracking performance of both swinging leg and CoM, whereas task-space tracking controllers, in practice, usually suffer from modeling/sensing errors. As a practical solution, we proposed to combine joint-space controllers as shown in the above control framework. Specifically, we encode the self-generated quasi-dynamic walking motions into some joint-, or higher-level oscillators. Then, we adapt the oscillator model through learning to increase the speed of the walking phase, leading to dynamic CNS+CPG walking. For the learning from static to dynamic motions, see the next section.

Baseball batting
We first studied a simple online learning algorithm with sequential least square method to predict the meeting time t^* and the position of the ball (x^*, z^*) on the cross section. The 3D ball position is recognized by the robot eye cameras (two foveal cameras), and the throwing timing is detected by the incoming velocity. During the ball detection and prediction the robot is supposed to be in quiet stance.
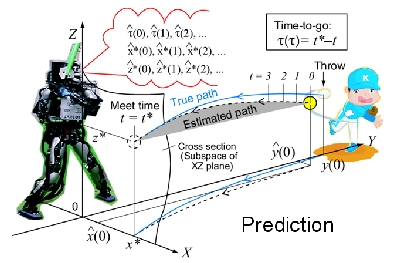
Fast swinging motions are generated as follows:
1) Apply cheap balancing control combined with G-comp and stiffness,
2) Superpose a simple PD-based tracking control for a family of minimum jerk upper-body trajectories whose via-points are set acc. the initial posture and different meeting positions of the bat.
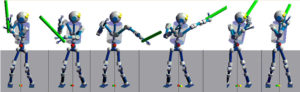

With this method, the robot could successfully hit the ball.
References
- S. Hyon, J. Morimoto and M. Kawato, From compliant balancing to dynamic walking on humanoid robot: Integration of CNS and CPG, 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, 2010, pp. 1084-1085. doi: 10.1109/ROBOT.2010.5509654
- Hyon, S., A motor control strategy with virtual musculoskeletal systems for compliant anthropomorphic robots, IEEE/ASME Transactions on Mechatronics, vol.14, issue 6, pp.677-688, 2009.
- Hyon, S., Learning external forces for human-humanoid interaction, Workshop for Young Researchers on Human-Friendly Robotics, Genoa, Dec, 2009.
- Hyon, S. and Fujimoto, K., Invariant manifold of symmetric orbits and its application toward globally optimal gait generation for biped locomotion, 9th International IFAC Symposium on Robot Control (SYROCO), Gifu, Japan, Sep. 2009, pp.619-626.
- Hyon, S., Osu, R. and Otaka, Y., Integration of multi-level postural balancing on humanoid robots, IEEE International Conference on Robotics and Automation, Kobe, Japan, May 2009, pp.1549-1556.
- Hyon, S., Iterative learning of dynamic full-body motions anchored by joint trajectories, The Workshop for IEEE International Conference on Robotics and Automation, Kobe, Japan, May 2009.
- Hyon, S., Compliant terrain adaptation for biped humanoids without measuring ground surface and contact forces, IEEE Transactions on Robotics, vol.25, no.1, pp. 171-178, 2009.
- Hyon, S., Moren, J. and Kawato, M., Toward humanoid batting: prediction and fast coordinated motion, Annual Conference of RSJ, AC2J2-01, Sep. 2008.
- Hyon, S., Moren, J. and Cheng, G., Humanoid batting with bipedal balancing, in Proceedings of IEEE-RAS International Conference on Humanoid Robots, pp.493-499, Daejon, Korea, Dec. 2008.
- Hyon, S., Morimoto, J. and Cheng, G., Hierarchical motor learning and synthesis with passivity-based controller and phase oscillator, IEEE International Conference on Robotics and Automation, pp. 2705-2710, May 2008.
- Hyon, S., Hale, J.G. and Cheng, G., Full-body compliant human-humanoid interaction: Balancing in the presence of unknown external forces, IEEE Transactions on Robotics, vol.23, no.5, pp.884-898, 2007.
- Hyon, S. and Cheng, G., Disturbance rejection for biped humanoids, in Proceedings of IEEE International Conference on Robotics and Automation, pp.2668-2675, Roma, Italy, April 2007. [ Paper | Video]
- Hyon, S. and Cheng, G., Gravity compensation and full-body balancing for humanoid robots, in Proceedings of IEEE-RAS International Conference on Humanoid Robots, pp.214-221, Genova, Italy, 2006.
- Hyon, S. and Cheng, G., Passivity-based full-body force control for humanoids and application to dynamic balancing and locomotion, in Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, pp.4915-4922, Beijing, China, 2006. [ Paper]
- Hyon, S. and Emura, T., Symmetric walking control: Invariance and global stability, IEEE International Conference on Robotics and Automation, pp.1455-1462, Barcelona, Spain, Apr. 2005.
- Hyon, S., Yokoyama, N. and Emura, T., Back handspring of a multi-link gymnastic robot - reference model approach, Advanced Robotics, vol. 20, no. 1, pp.93-113, 2006.
- Hyon, S. and Emura, T., Aerial posture control for 3D biped running using compensator around yaw axis, Proc. of IEEE ICRA, pp.57-62, Taipei, Taiwan, Sep 2003.
- Hyon, S., Emura, T. and Mita, T., Dynamics-based control of one-legged hopping robot, Journal of Systems and Control Engineering, Proceedings of the Institution of Mechanical Engineers Part I, pp.83-98, 2003.
- Hyon, S., Development and Control of One-Legged Hopping Robot, Ph.D thesis, Tokyo Institute of Technology, 2002.
- Setiawan, S. A., Hyon, S., Yamaguchi, J. and Takanishi, A., Physical interaction between human and a bipedal humanoid robot -Realization of human-follow walking-, Proc. of IEEE International Conference on Robotics and Automation, pp. 361-367, 1999.
(see Hyon, S., Physical interaction between human and a bipedal humanoid robot - realization of human-follow walking -, MS thesis, Waseda University, 1997, for more details)
Technical Contributors
- Force controller implementation was done with Dr. Gordon Cheng. He provided the real-time communication software for both robots.
- Idea of frequency modulation of CPG was borrowed from Dr. Jun Morimoto. He first demonstrated a biped walking experiment using the idea.
He also provided a template of the simulator (SD/FAST + OpenGL). - We maintain our hardwires with the help of Mr. Nao Nakano.
- Vision part of the initial baseball demo was done with Dr. Jan Moren.
Acknowledgements
- All the works here are supervised by Dr. Mitsuo Kawato, the Director of Computational Neuroscience Laboratories, ATR, Japan.
- The robots are with ATR or NICT. All the works here are conducted by S. Hyon at ATR or NICT as a researcher (2005-2009), or as a visiting researcher (2010-).
- We thank the support of National Institute of Information and Communications Technology (NICT). The humanoid robot I-1 (blue one) is developed by NICT in the collaborative research project with ATR.
- We thank the support of Japan Science and Technology Agency (JST). The humanoid robot CB-i (gray one) is developed by JST, ICORP, Computational Brain Project (2004.1-2009.3).
- We wish to acknowledge the support of the members of SARCOS. The both robots were fabricated by SARCOS. Dr. Gordon Cheng organized this development as the department head of HRCN, CNS, ATR.
- We wish to acknowledge Sankyoku Co., Ltd. and Mori Kougyou Co., Ltd. for their continuous support on hydraulic systems for more than decade.
2025/01/29



